Read the Following Scales to the Correct Number of Significant Figures Worksheet B

i Units and Measurement

1.half dozen Significant Figures

Learning Objectives

By the end of this section, yous will be able to:

Decide the right number of significant figures for the outcome of a computation.
Draw the relationship between the concepts of accuracy, precision, dubiety, and discrepancy.
Calculate the percentage doubtfulness of a measurement, given its value and its doubt.
Determine the uncertainty of the event of a computation involving quantities with given uncertainties.

(Figure) shows two instruments used to measure the mass of an object. The digital scale has by and large replaced the double-pan balance in physics labs because it gives more accurate and precise measurements. Only what exactly exercise we mean by authentic and precise? Aren't they the same matter? In this section we examine in item the procedure of making and reporting a measurement.

Figure a shows an old rusted double-pan balance with a standard mass on one pan. Figure b shows a modern digital analytical balance. — **Figure i.11** (a) A double-pan mechanical balance is used to compare dissimilar masses. Normally an object with unknown mass is placed in 1 pan and objects of known mass are placed in the other pan. When the bar that connects the 2 pans is horizontal, then the masses in both pans are equal. The "known masses" are typically metal cylinders of standard mass such as ane g, 10 g, and 100 g. (b) Many mechanical balances, such as double-pan balances, accept been replaced by digital scales, which can typically measure the mass of an object more precisely. A mechanical balance may read only the mass of an object to the nearest tenth of a gram, merely many digital scales can mensurate the mass of an object upwardly to the nearest thousandth of a gram. (credit a: modification of work by Serge Melki; credit b: modification of work by Karel Jakubec)

Accuracy and Precision of a Measurement

Science is based on observation and experiment—that is, on measurements. Accuracy is how shut a measurement is to the accepted reference value for that measurement. For example, permit'due south say we want to measure the length of standard printer paper. The packaging in which nosotros purchased the paper states that information technology is 11.0 in. long. Nosotros so measure out the length of the paper iii times and obtain the post-obit measurements: 11.1 in., eleven.2 in., and 10.nine in. These measurements are quite accurate because they are very close to the reference value of 11.0 in. In contrast, if we had obtained a measurement of 12 in., our measurement would not be very accurate. Discover that the concept of accuracy requires that an accustomed reference value be given.

The precision of measurements refers to how close the understanding is betwixt repeated independent measurements (which are repeated under the same conditions). Consider the example of the paper measurements. The precision of the measurements refers to the spread of the measured values. 1 fashion to analyze the precision of the measurements is to determine the range, or difference, betwixt the lowest and the highest measured values. In this case, the lowest value was 10.9 in. and the highest value was xi.2 in. Thus, the measured values deviated from each other by, at virtually, 0.3 in. These measurements were relatively precise because they did not vary besides much in value. Withal, if the measured values had been 10.nine in., 11.1 in., and 11.9 in., and then the measurements would not be very precise because at that place would be significant variation from i measurement to another. Observe that the concept of precision depends simply on the bodily measurements acquired and does not depend on an accepted reference value.

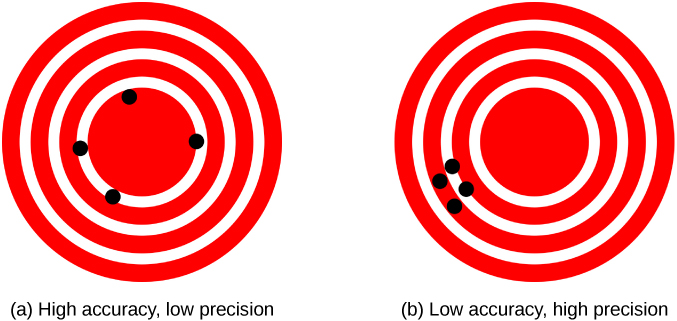
The measurements in the newspaper example are both accurate and precise, only in some cases, measurements are accurate merely not precise, or they are precise merely non accurate. Let's consider an example of a GPS attempting to locate the position of a eating place in a city. Call up of the restaurant location as existing at the center of a balderdash's-eye target and retrieve of each GPS attempt to locate the eating place equally a black dot. In (Figure)(a), we come across the GPS measurements are spread out far autonomously from each other, but they are all relatively shut to the actual location of the eatery at the center of the target. This indicates a low-precision, high-accuracy measuring system. However, in (Effigy)(b), the GPS measurements are concentrated quite closely to one another, but they are far away from the target location. This indicates a high-precision, low-accuracy measuring organisation.

Two target patterns, each consisting of three white concentric rings on a red background. Figure a, labeled — **Figure one.12** A GPS attempts to locate a restaurant at the eye of the bull'southward-heart. The black dots stand for each attempt to pinpoint the location of the restaurant. (a) The dots are spread out quite far autonomously from i another, indicating depression precision, just they are each rather shut to the bodily location of the restaurant, indicating loftier accurateness. (b) The dots are full-bodied rather closely to i another, indicating high precision, but they are rather far away from the actual location of the restaurant, indicating low accuracy. (credit a and credit b: modification of works by Dark Evil)

Accuracy, Precision, Uncertainty, and Discrepancy

The precision of a measuring system is related to the uncertainty in the measurements whereas the accurateness is related to the discrepancy from the accepted reference value. Uncertainty is a quantitative measure of how much your measured values deviate from one another. In that location are many different methods of calculating uncertainty, each of which is advisable to different situations. Some examples include taking the range (that is, the biggest less the smallest) or finding the standard deviation of the measurements. Discrepancy (or "measurement mistake") is the deviation between the measured value and a given standard or expected value. If the measurements are not very precise, then the doubt of the values is high. If the measurements are not very accurate, then the discrepancy of the values is high.

Recall our example of measuring newspaper length; we obtained measurements of xi.1 in., xi.ii in., and x.9 in., and the accepted value was 11.0 in. We might average the 3 measurements to say our best guess is 11.1 in.; in this case, our discrepancy is eleven.1 – 11.0 = 0.1 in., which provides a quantitative measure of accuracy. We might calculate the uncertainty in our best guess by using the range of our measured values: 0.3 in. And then we would say the length of the paper is eleven.1 in. plus or minus 0.3 in. The dubiousness in a measurement, A, is often denoted as δA (read "delta A"), and then the measurement upshot would exist recorded as A ± δA. Returning to our paper instance, the measured length of the paper could exist expressed as eleven.1 ± 0.iii in. Since the discrepancy of 0.i in. is less than the doubt of 0.3 in., we might say the measured value agrees with the accepted reference value to inside experimental doubt.

Some factors that contribute to uncertainty in a measurement include the following:

Limitations of the measuring device
The skill of the person taking the measurement
Irregularities in the object being measured
Whatsoever other factors that bear on the outcome (highly dependent on the situation)

In our example, such factors contributing to the uncertainty could be the smallest division on the ruler is 1/16 in., the person using the ruler has bad eyesight, the ruler is worn downwardly on 1 cease, or one side of the paper is slightly longer than the other. At any rate, the dubiousness in a measurement must exist calculated to quantify its precision. If a reference value is known, it makes sense to calculate the discrepancy as well to quantify its accurateness.

Percent incertitude

Some other method of expressing uncertainty is as a percent of the measured value. If a measurement A is expressed with uncertainty δA, the percentage uncertainty is divers as

$\text{Percent uncertainty}=\frac{\delta A}{A}\,×\,100%.$

Example

Calculating Percentage Dubiousness: A Bag of Apples

A grocery store sells 5-lb bags of apples. Let's say we purchase four numberless during the course of a month and counterbalance the bags each time. We obtain the following measurements:

Calendar week i weight: 4.8 lb
Calendar week 2 weight: 5.3 lb
Week 3 weight: 4.9 lb
Week 4 weight: 5.4 lb

We so decide the average weight of the 5-lb bag of apples is 5.one ± 0.2 lb. What is the percentage uncertainty of the bag's weight?

Strategy

Start, observe that the average value of the bag's weight, A, is 5.i lb. The uncertainty in this value,

$\delta A,$

is 0.2 lb. We tin use the following equation to decide the percentage dubiety of the weight:

$\text{Percent uncertainty}=\frac{\delta A}{A}\,×\,100%.$

Solution

Substitute the values into the equation:

$\text{Percent uncertainty}=\frac{\delta A}{A}\,×\,100%=\frac{0.2\,\text{lb}}{5.1\,\text{lb}}\,×\,100%=3.9%\approx 4%.$

SignificanceWe tin conclude the average weight of a handbag of apples from this store is 5.1 lb ± iv%. Notice the per centum dubiousness is dimensionless because the units of weight in

$\delta A=0.2$

lb canceled those in A = 5.1 lb when we took the ratio.

Bank check Your Understanding

A high school rails coach has simply purchased a new stopwatch. The stopwatch transmission states the stopwatch has an uncertainty of ±0.05 southward. Runners on the track omnibus'due south team regularly clock 100-grand sprints of 11.49 s to xv.01 due south. At the school'southward final track run across, the first-place sprinter came in at 12.04 south and the second-place sprinter came in at 12.07 s. Volition the coach's new stopwatch exist helpful in timing the dart team? Why or why not?

[reveal-answer q="fs-id1168328204335″]Testify Solution[/reveal-reply]

[subconscious-answer a="fs-id1168328204335″]

No, the autobus'southward new stopwatch will not exist helpful. The incertitude in the stopwatch is also dandy to differentiate between the dart times effectively.

[/hidden-answer]

Uncertainties in calculations

Uncertainty exists in anything calculated from measured quantities. For example, the area of a flooring calculated from measurements of its length and width has an dubiousness because the length and width have uncertainties. How large is the incertitude in something you calculate by multiplication or division? If the measurements going into the adding have small uncertainties (a few percent or less), and then the method of adding percents tin be used for multiplication or division. This method states the percentage uncertainty in a quantity calculated by multiplication or division is the sum of the percent uncertainties in the items used to make the calculation. For case, if a floor has a length of 4.00 m and a width of 3.00 m, with uncertainties of ii% and i%, respectively, then the area of the floor is 12.0 m² and has an incertitude of 3%. (Expressed as an area, this is 0.36 one thousandⁱⁱ [

$12.0{\,\text{m}}^{2}\,×\,0.03$

], which nosotros round to 0.4 chiliad² since the surface area of the floor is given to a tenth of a foursquare meter.)

Precision of Measuring Tools and Significant Figures

An important gene in the precision of measurements involves the precision of the measuring tool. In full general, a precise measuring tool is i that can measure values in very small increments. For example, a standard ruler can measure length to the nearest millimeter whereas a caliper can measure length to the nearest 0.01 mm. The caliper is a more precise measuring tool because it can mensurate extremely modest differences in length. The more precise the measuring tool, the more precise the measurements.

When we limited measured values, we can but list every bit many digits as we measured initially with our measuring tool. For example, if nosotros use a standard ruler to measure the length of a stick, we may measure out information technology to be 36.seven cm. Nosotros tin can't express this value as 36.71 cm because our measuring tool is not precise plenty to measure a hundredth of a centimeter. Information technology should exist noted that the last digit in a measured value has been estimated in some way by the person performing the measurement. For example, the person measuring the length of a stick with a ruler notices the stick length seems to be somewhere in between 36.6 cm and 36.seven cm, and he or she must guess the value of the last digit. Using the method of significant figures, the rule is that the terminal digit written downwards in a measurement is the starting time digit with some uncertainty. To determine the number of pregnant digits in a value, get-go with the first measured value at the left and count the number of digits through the last digit written on the right. For instance, the measured value 36.seven cm has three digits, or three significant figures. Pregnant figures point the precision of the measuring tool used to measure out a value.

Zeros

Special consideration is given to zeros when counting significant figures. The zeros in 0.053 are not pregnant because they are placeholders that locate the decimal indicate. There are 2 significant figures in 0.053. The zeros in 10.053 are non placeholders; they are significant. This number has 5 significant figures. The zeros in 1300 may or may not be pregnant, depending on the style of writing numbers. They could hateful the number is known to the last digit or they could exist placeholders. So 1300 could have two, three, or four significant figures. To avoid this ambiguity, we should write 1300 in scientific note every bit

$1.3\,×\,{10}^{3},$

$1.30\,×\,{10}^{3},$

$1.300\,×\,{10}^{3},$

depending on whether information technology has two, iii, or iv pregnant figures. Zeros are significant except when they serve only as placeholders.

Meaning figures in calculations

When combining measurements with dissimilar degrees of precision, the number of significant digits in the final answer can be no greater than the number of significant digits in the least-precise measured value. At that place are ii different rules, one for multiplication and segmentation and the other for add-on and subtraction.

For multiplication and partition, the event should have the same number of significant figures as the quantity with the to the lowest degree number of pregnant figures inbound into the calculation. For example, the expanse of a circle can exist calculated from its radius using A = πr ². Let'southward see how many significant figures the surface area has if the radius has only two—say, r = 1.2 m. Using a calculator with an eight-digit output, we would calculate
$A=\pi {r}^{2}=(3.1415927\text{…})\,×\,{(1.2\,\text{m})}^{2}=4.5238934{\,\text{m}}^{2}.$

But considering the radius has but two significant figures, it limits the calculated quantity to two significant figures, or

$A=4.5{\,\text{m}}^{2},$

although π is good to at least viii digits.
For improver and subtraction, the reply can contain no more decimal places than the to the lowest degree-precise measurement. Suppose we buy 7.56 kg of potatoes in a grocery store equally measured with a scale with precision 0.01 kg, then we drop off half dozen.052 kg of potatoes at your laboratory as measured past a scale with precision 0.001 kg. Then, we go habitation and add together thirteen.vii kg of potatoes as measured by a bathroom calibration with precision 0.1 kg. How many kilograms of potatoes practice we now take and how many significant figures are appropriate in the answer? The mass is found by simple improver and subtraction:
$\begin{array}{cc} \phantom{\rule{1.2em}{0ex}}7.56\,\text{kg}\hfill \\ -6.052\,\text{kg}\hfill \\ \\ \\ \,\frac{\,+13.7\,\text{kg}}{15.208\,\text{kg}}=15.2\,\text{kg}\text{.}\hfill \end{array}$

Next, we place the least-precise measurement: 13.7 kg. This measurement is expressed to the 0.one decimal place, and so our terminal respond must also be expressed to the 0.1 decimal identify. Thus, the reply is rounded to the tenths place, giving us 15.2 kg.

Pregnant figures in this text

In this text, most numbers are assumed to take three significant figures. Furthermore, consistent numbers of significant figures are used in all worked examples. An respond given to 3 digits is based on input good to at least three digits, for instance. If the input has fewer significant figures, the respond will also have fewer significant figures. Care is also taken that the number of pregnant figures is reasonable for the situation posed. In some topics, especially in eyes, more than accurate numbers are needed and we apply more than than three pregnant figures. Finally, if a number is exact, such every bit the two in the formula for the circumference of a circle, C = 2πr, it does non affect the number of significant figures in a calculation. Too, conversion factors such equally 100 cm/1 m are considered verbal and exercise not touch on the number of significant figures in a calculation.

Summary

Accuracy of a measured value refers to how close a measurement is to an accepted reference value. The discrepancy in a measurement is the amount by which the measurement result differs from this value.
Precision of measured values refers to how close the agreement is between repeated measurements. The uncertainty of a measurement is a quantification of this.
The precision of a measuring tool is related to the size of its measurement increments. The smaller the measurement increment, the more precise the tool.
Meaning figures express the precision of a measuring tool.
When multiplying or dividing measured values, the concluding reply tin contain merely as many significant figures every bit the least-precise value.
When calculation or subtracting measured values, the last reply cannot contain more decimal places than the to the lowest degree-precise value.

Key Equations

Percent doubt

$\text{Percent uncertainty}=\frac{\delta A}{A}\,×\,100%$

Conceptual Questions

(a) What is the relationship between the precision and the uncertainty of a measurement? (b) What is the relationship betwixt the accurateness and the discrepancy of a measurement?

[reveal-reply q="fs-id1168328247310″]Show Solution[/reveal-answer]

[hidden-reply a="fs-id1168328247310″]

a. Doubt is a quantitative measure of precision. b. Discrepancy is a quantitative measure of accuracy.

[/hidden-respond]

Problems

Consider the equation 4000/400 = 10.0. Assuming the number of meaning figures in the answer is right, what can you say about the number of significant figures in 4000 and 400?

Suppose your bathroom scale reads your mass as 65 kg with a 3% dubiousness. What is the uncertainty in your mass (in kilograms)?

ii kg

A good-quality measuring tape tin can be off by 0.50 cm over a distance of twenty one thousand. What is its percent doubt?

An infant'southward pulse rate is measured to be 130 ± 5 beats/min. What is the percent uncertainty in this measurement?

(a) Suppose that a person has an average heart rate of 72.0 beats/min. How many beats does he or she have in 2.0 years? (b) In two.00 years? (c) In ii.000 years?

A can contains 375 mL of soda. How much is left after 308 mL is removed?

[reveal-answer q="fs-id1168328295068″]Show Solution[/reveal-respond]

[subconscious-answer a="fs-id1168328295068″]

67 mL

[/hidden-answer]

State how many pregnant figures are proper in the results of the post-obit calculations: (a)

$(106.7)(98.2)/(46.210)(1.01);$

(b)

${(18.7)}^{2};$

(c)

$(1.60\,×\,{10}^{-19})(3712)$

(a) How many significant figures are in the numbers 99 and 100.? (b) If the doubtfulness in each number is 1, what is the per centum uncertainty in each? (c) Which is a more meaningful way to express the accuracy of these ii numbers: significant figures or percentage uncertainties?

[reveal-reply q="fs-id1168327948324″]Prove Solution[/reveal-answer]

[subconscious-answer a="fs-id1168327948324″]

a. The number 99 has 2 pregnant figures; 100. has iii significant figures. b. i.00%; c. percentage uncertainties

[/hidden-answer]

(a) If your speedometer has an uncertainty of ii.0 km/h at a speed of 90 km/h, what is the percent uncertainty? (b) If information technology has the same per centum uncertainty when it reads 60 km/h, what is the range of speeds you could be going?

(a) A person'due south blood force per unit area is measured to be

$120±2\,\text{mm Hg}.$

What is its percent uncertainty? (b) Bold the same percent uncertainty, what is the uncertainty in a claret pressure measurement of 80 mm Hg?

a. 2%; b. i mm Hg

A person measures his or her heart charge per unit by counting the number of beats in xxx s. If 40 ± 1 beats are counted in 30.0 ± 0.5 s, what is the middle rate and its uncertainty in beats per minute?

What is the area of a circle 3.102 cm in diameter?

[reveal-answer q="fs-id1168328249411″]Evidence Solution[/reveal-answer]

[hidden-reply a="fs-id1168328249411″]

7.557 cmⁱⁱ

[/subconscious-answer]

Determine the number of meaning figures in the following measurements: (a) 0.0009, (b) 15,450.0, (c) 6×x^three, (d) 87.990, and (east) thirty.42.

Perform the post-obit calculations and limited your reply using the right number of meaning digits. (a) A woman has two numberless weighing thirteen.5 lb and one bag with a weight of ten.2 lb. What is the full weight of the bags? (b) The strength F on an object is equal to its mass grand multiplied past its acceleration a. If a wagon with mass 55 kg accelerates at a charge per unit of 0.0255 grand/s², what is the force on the wagon? (The unit of force is called the newton and it is expressed with the symbol N.)

[reveal-answer q="fs-id1168328280169″]Show Solution[/reveal-reply]

[hidden-answer a="fs-id1168328280169″]

a. 37.2 lb; because the number of bags is an exact value, information technology is not considered in the significant figures; b. 1.iv N; considering the value 55 kg has just 2 significant figures, the final value must also contain two significant figures

[/subconscious-respond]

Glossary

accuracy: the degree to which a measured value agrees with an accepted reference value for that measurement

discrepancy: the divergence between the measured value and a given standard or expected value

method of adding percents: the percent uncertainty in a quantity calculated past multiplication or sectionalisation is the sum of the percent uncertainties in the items used to make the adding.

percent dubiety: the ratio of the dubiety of a measurement to the measured value, expressed as a pct

precision: the degree to which repeated measurements concord with each other

meaning figures: used to limited the precision of a measuring tool used to measure a value

dubiety: a quantitative measure out of how much measured values deviate from one another

clantonpashery.blogspot.com

Source: https://opentextbc.ca/universityphysicsv1openstax/chapter/1-6-significant-figures/

Read the Following Scales to the Correct Number of Significant Figures Worksheet B

1.half dozen Significant Figures

Learning Objectives

Accuracy and Precision of a Measurement

Accuracy, Precision, Uncertainty, and Discrepancy

Percent incertitude

Example

Calculating Percentage Dubiousness: A Bag of Apples

Strategy

Solution

Bank check Your Understanding

Uncertainties in calculations

Precision of Measuring Tools and Significant Figures

Zeros

Meaning figures in calculations

Pregnant figures in this text

Summary

Key Equations

Conceptual Questions

Problems

Glossary

0 Response to "Read the Following Scales to the Correct Number of Significant Figures Worksheet B"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel